Liquid water content (LWC), is the mass of liquid water in a unit volume of air.  LWC can be determined based on the principle that the latent heat is required to evaporate water.  If a metal coil, connected to an electic circuit,  is exposed to the air in a cloud and is heated to a temperature high enough to quickly evaporate water then the latent heat will be supplied by the coil.  If the coil were to maintain a constant temperature then power would have to be supplied if heat is being removed by the water droplets.  This power is proportional to the LWC in cloud.  The total power supplied to the coil is the sum of two components called the wet and dry terms of the power.  The wet term is the power supplied due to the heat supplied to the droplets to heat them to boiling point and to vaporize them.  The dry term is the power supplied due to the transfer of heat to surrounding air molecules due to the difference in temperature between the coil and the air.  The two term are made up of variables which are measured by the aircraft.

The equation for the total power supplied to the coil is:

. (1)

The equations for the wet and dry terms of the power are:

(2)

where C and x are calibration constants, Ts is the temperature of the sensor, Ta is the ambient air temperature, p is the atmospheric pressure, and v is the true air speed, and

(3)

where LWC is the liquid water content, l is the length of the sensor, d is the diameter of the sensor, v is the true air speed, Lv is the latent heat of vaporization, cw is the specific heat of liquid water, and Tsw is the temperature at which water vaporizes off the coil, which is assumed to be 90 degrees Celsius.  When (2) and (3) are substituted into (1) the new equation for the total power is:

. (4)

The equation for the liquid water content is found by rearranging the terms and solving for LWC,  yielding

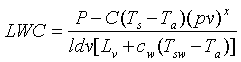. (5)

As stated in the calibration procedures page, a correction term has to be added to the dry term of the power.  The is because a plot of the king voltage, which is one tenth of the king power, versus true air speed, out of cloud, does not pass through [0,0].  This suggests that if the velocity of the plane is zero the voltage, and subsiquently the power, of the dry term would not be zero.  With this new constant added the equation becomes

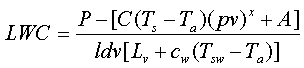(6)

 Continue to Calibration Procedures page

 Back to Main page